¿Cómo se mide la audiencia televisiva?

¿Cúantas veces habéis visto por televisión que tal programa tuvo X audiencia? ¿Alguna vez os habéis preguntado como obtienen esta cifra? Pues hoy voy a tratar este tema de manera muy breve.

La mayoría de las personas a las que les he hecho esta pregunta, responden que el televisor transmite los datos. Esto es incorrecto.

La siguiente imagen que voy a mostrarles, es para que puedan ver de manera sencilla, la recepción de las ondas:

Las ondas son captadas por la antena, es ahí cuando estas son decodificadas en el decodificador TDT, este puede estar integrado o no, en el televisor. El televisor luego procesa la señal decodificada y la muestra por pantalla.

Tal y como se muestra aquí, no hay transmisor ninguno, por lo que no se puede transmitir dicha información, además de que no sería fiable ya que se podría replicar la señal.

Entonces…

¿Cómo se calcula la audiencia?

La solución se encuentra en la estadística, y es que se puede estimar la audiencia de una población a partir de una muestra representativa de esta.

Kantar Media, es la empresa que se encarga de realizar esto, por lo menos en España, en otros países desconozco se actuará o no. De manera aleatoria, Kantar Media ha repartido unos audímetros en 4625 hogares, cada cual representa a una población de unas 10000 personas. Por lo que sólo 4625 hogares son los responsables de representar a los 46 millones de españoles. Estos aparatos se encargan de enviar la información de que cadenas se ven, y durante cuanto tiempo.

Seguramente estén pensando que esto esta mal, ¿cómo puede ser que tan pocos hogares puedan representar todo? Pero realmente los datos son correctos, y además nos dicen con que margen de error estamos obteniendo dichos resultados. Por lo general, cuando se busca estimar algo, intervienen 3 variables:

• Intervalo de confianza
• Margen de error
• Tamaño de la muestra

Estas 3 variables estan relacionadas entre sí, por lo que un cambio en una de ellas afectaría al valor de las otras dos. Realmente, a nosotros nos interesa un intervalo de confianza idealmente del 100%, por lo que el margen de error es nulo, pero eso nos obliga a tener una tamaño de la muestra igual que la población, y eso en términos ecónomicos es muy costoso.

La forma en que disminuye la probabilidad a medida que me alejo de la media corresponde a una distribución gaussiana. Podemos fijar un intervalo alrededor del valor más probable, de manera que englobemos el 95% de la probabilidad (nivel de confianza). La distancia a la que me tengo que alejar del valor más probable para englobar este 95% determina el margen de error.

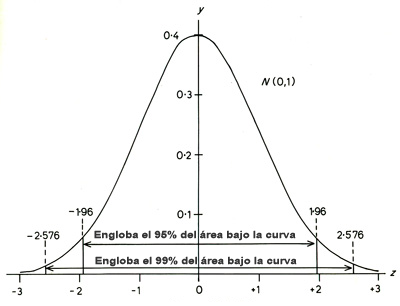
Cuando se hacen estas mediciones de audiencia, se realizan con un margen de error entre el 1% y el 5%.

Calculemos de manera teórica cual tendría que ser el tamaño de nuestra muestra para un intervalo de confianza del 95%

$$n = \frac { N\cdot Z^{ 2 }\cdot p\cdot (1-p) }{ (N-1)\cdot { e }^{ 2 }+{ Z }^{ 2 }\cdot p\cdot (1-p) }$$

Donde:

• \( N \), es el tamaño de la población
• \( n \), es el tamaño de la muestra
• \( Z \), Es la desviación del valor medio que aceptamos para lograr el nivel de confianza deseado.
• \( e \), es el margen de error que admito
• \( p \), es la proporción que esperamos encontrar. Como no tengo ninguna información del valor que espero, ajustaremos esto al 50%

En la tabla de valores Z, tenemos que para un intervalo de confianza del 95%, \( Z = 1,96 \). Por lo que:

\[ n\quad =\quad \frac { 46\cdot { 10 }^{ 6 }\cdot 1,96^{ 2 }\cdot 0.5\cdot (1-0.5) }{ (46\cdot { 10 }^{ 6 }-1)\cdot { 0.05 }^{ 2 }+{ 1,96 }^{ 2 }\cdot 0.5\cdot (1-0.5) } =\quad 384 \]

Es decir, que bastaría sólo 384 muestras para determinar la audiencia de un programa en España. Vamos a aumentar el intervalo de confianza, y por ende bajar el margen de error, y veamos cuantas muestras son necesarias. Probaremos con un margen de error del 2%:

\[ n\quad =\quad \frac { 46\cdot { 10 }^{ 6 }\cdot 2,38^{ 2 }\cdot 0.5\cdot (1-0.5) }{ (46\cdot { 10 }^{ 6 }-1)\cdot 0.02^{ 2 }+{ 2,38 }^{ 2 }\cdot 0.5\cdot (1-0.5) } =\quad 3540 \]

Por lo que podemos observar, aumenta de manera significativa el tamaño de la muestra que se debería tomar, por lo que Kantar Media supongo que estará jugando entre estos valores, y seguramente harán algún que otro ajuste.

Obviamente, para la fiabilidad de estos resultados, debemos asegurarnos que las muestras sean representativas, y escogidas de manera aleatoria.

Así que eso… Así saben las cadenas cuanta audiencia tienen. Sé que este post ha sido algo off-topic de las cosas que suelo comentar por aquí, pero ha estado entretenido.

Espero que les haya gustado.

¡Un saludo!